Gastbeitrag von Frank Bosse
Während die Auseinandersetzung über den nicht vorhandenen Aufwärtstrend in den globalen Temperaturen der letzten 16 Jahre seit 1995 nach den Aufzeichnungen der CRU (HadCRUT4) noch im Gange ist, hat sich etwas womöglich viel Weitreichenderes getan.
Im Jahre 2011 erschien eine Arbeit von Santer und Kollegen, in der sie beschrieben, dass es mindestens eines 17 Jahre langen Trends bedarf, um die menschlichen Einflüsse auf die mittlere Temperatur der Troposphäre zu identifizieren. In der Zusammenfassung der Arbeit ist zu lesen:
“Our results show that temperature records of at least 17 years in length are required for identifying human effects on global-mean tropospheric temperature.”
Dabei wurde die Temperaturreihe “TLT” ( Temperature lower Troposphere) namentlich angesprochen. Wir können uns diese Reihe – sie wird monatlich erhoben – betrachten:
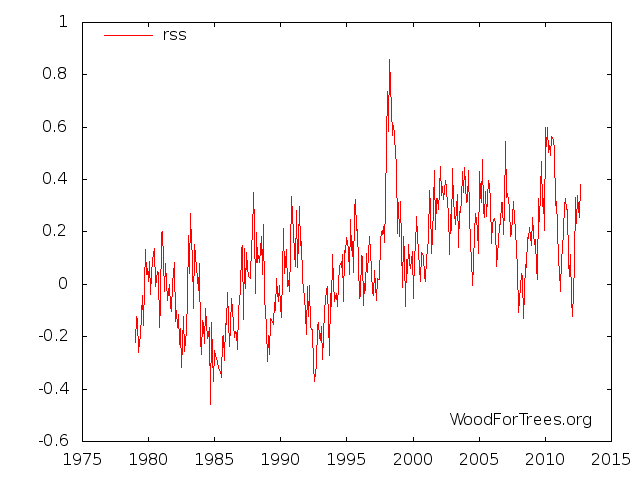
Es kommt nun ein Sachverhalt zum Tragen, den man Autokorrelation nennt. Was bedeutet das? Machen wir ein Beispiel: Sie wollen den Temperaturverlauf des Wassers in einem 10 l-Eimer durch einem linearen Trend beschreiben. Es ist klar, dass die Temperaturänderung recht langsam verläuft, da Wasser eine hohe Wärmeträgheit aufweist. Sie haben 1h Zeit, einen Trend nachzuweisen. Nehmen wir an, Sie messen alle 10 min und nehmen die Werte auf. Das ergibt am Ende eine Reihe mit 6 Messwerten und die Regressionsrechnung zeigt, dass es einen Trend gibt, dieser jedoch auch zufällig sein kann. In der Statistik ist die Frage zu beantworten: Ist der Trend positiv und zwar nicht etwa zufällig sondern ist er es nachprüfbar und auf eine echte Erwärmung zurückzuführen? Wenn ja: dann ist der Trend signifikant. Mit dem Zufall ist es so ein Ding, man begrenzt ihn, indem man fordert: zu 95% muss der Trend „echt“ sein, nur 5% lassen wir dem Zufall übrig. In der Statistik nennt man das ein 95%-Konfidenzintervall.
Mit den 6 Messwerten, die Sie oben gemessen haben, können Sie nun diese Bedingung nicht erfüllen. Nun kommen Sie auf die Idee, nicht alle 10 min zu messen, sondern jede Minute. Sie haben dann 60 Messwerte und schaffen es so, einen signifikanten Trend nachzuweisen. Ist er aber auch „echt“ im Sinne der Physik? Oder haben Sie nur eine Wiederholung der eigentlich mehr oder weniger selben Messwerte erzeugt und so eine scheinbare Signifikanz eingetragen?
Dafür gibt es in der Statistik Tests, die ausweisen, ob die Messwerte zu stark voneinander abhängig sind oder nicht. Diese Abhängigkeit eines Messwertes vom vorigen nennt man Autokorrelation.
Wenden wir nun einen Test (den von Durbin und Watson, es gibt ihn seit 1951) auf die Temperatur der unteren Troposphäre (TLT) an. Wir sehen, dass die monatlichen Werte zu „dicht“ gesetzt sind. Mit ein wenig Sicherheit können wir die Autokorrelation ausschließen, wenn wir nur 6-monatige Mittelwerte berücksichtigen.
In der oben zitierten Arbeit ist die kritische Grenze 17 Jahre. Um sicher zu gehen, wollen wir die letzten 18 Jahre untersuchen, das sind die Monate von September 1994 bis August 2012, also insgesamt 216. Wir bilden die 6-monatigen Mittelwerte dieser Reihe und berechnen, ob der Trend signifikant positiv auf dem 95%-Niveau ist. Wenn das so sein soll, dann müssen beide Grenzwerte der Trendsteigerungen positiv sein. Sind sie es?
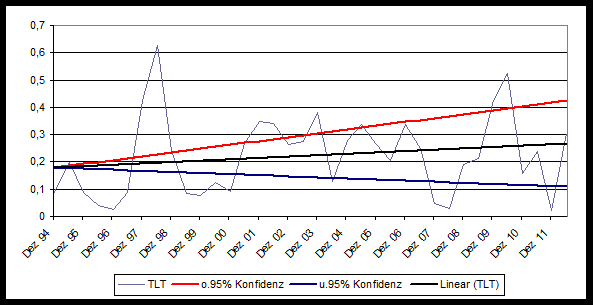
Nein! Der mittlere Trend ( schwarz) ist zwar noch positiv, aber er ist nicht signifikant. Der untere ( blau) ist negativ. Es ist damit gezeigt, dass die Bedingung von Santer u.a. in ihrer Arbeit seit September 1994 nicht mehr gegeben ist, wenn die Autokorrelation berücksichtigt wird. Und das muss sie.
Seit 18 Jahren hat sich die Temperatur der Troposphäre nicht mehr signifikant erhöht.
Und mehr noch. Untersuchen wir den Verlauf der Oberflächentemperaturen der Meere, man kann sie hier anzeigen lassen seit 1995:
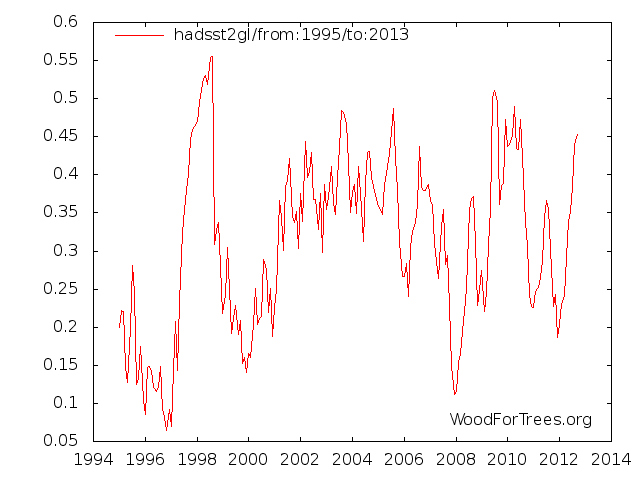
Wir unterstellen, dass sich die Temperatur auf dem (hohen) Niveau des August 2012 bis Dezember hält, schließlich war es im August recht warm, da sich ein El Nino ankündigte, der wohl doch nicht kommen wird. Man soll uns ja nicht cherry-picking vorwerfen. Der Trend ist da (0,067 Grad pro Jahrzehnt), aber er ist nicht signifikant positiv auf dem 95-Prozent Konfidenzniveau, wenn man jährliche Mittelwerte benutzt. Das muss man hier jedoch, vergleiche das Bild mit dem Eimer Wasser oben.
Auch die Temperaturen der gesamten Wasseroberfläche haben sich in den letzten 18 Jahren nicht signifikant erhöht.
Was bedeutet das? Hat der Mensch nicht mehr Einfluss genommen auf die Temperaturen der Troposphäre und der Wasseroberfläche? Mit Sicherheit hat er das, er hat schließlich seitdem immer weiter CO2 produziert. Der Gehalt an Kohlendioxid in der Luft hat sich seit 1995 von 359 ppm auf 397 ppm erhöht. Nach den Modellen des IPCC hätten sich dann auch die Temperaturen von Troposphäre und Wasseroberfläche signifikant erhöhen müssen, das haben sie jedoch nicht. Dabei spielt die natürliche Variabilität z.B. durch ENSO auch eine Rolle. Aber kann die Sensitivität gegenüber CO2 so groß sein wie angenommen? 3,2K pro Verdopplung des CO2-Gehaltes? Zwei Beiträge der jüngsten Vergangenheit sprechen dagegen: Der eine kommt nach Untersuchung der Strahlungsbilanz beim Ausbruch des Vulkans Pinatobu 1991 auf einen Wert von 1,4K, der andere bei Auswertung der Globalen Temperaturen und des Wärmeinhaltes der oberen 2000 m Wasser der Ozeane ( OHC) auf 1,7K.
Was ist wahrscheinlicher? 3,2K wie die Klimasensivität für CO2 vom IPCC geschätzt wird oder um 1,6K? Die Erfüllung des „berühmten“ Santerschen Postulats für die Temperaturen der Troposphäre und der Wasseroberflächen sollte für das Letztere sprechen. Was wieder zum Ausgangspunkt von „Die kalte Sonne“ führt: Der anthropogene Anteil an der Erwärmung ist da, wahrscheinlich ist er jedoch nur halb so groß wie vom IPCC angenommen.



